CRYSTAL STRUCTURE
Solids are of two types: Amorphous and crystalline. In amorphous solids, there is no order in the arrangement of their constituent atoms (molecules). Hence no definite structure could be assigned to them. A substance is said to be crystalline when the arrangement of the units (atoms, molecules or ions) of matter inside it is regular and periodic.
Space lattice
An array of points which describe the three dimensional arrangement of particles (atoms, molecules or ions) in a crystal structure is called space lattice. Here environment about each point should be identical.
Basis
A crystal structure is formed by associating with every lattice point a unit assembly of units or molecules identical in composition. This unit assembly is called basis.
A crystal structure is formed by the addition of a basis to every lattice point.
I.e., lattice + Basis = crystal structure.
Thus the crystal structure is real and the crystal lattice is imaginary.

Solids are of two types: Amorphous and crystalline. In amorphous solids, there is no order in the arrangement of their constituent atoms (molecules). Hence no definite structure could be assigned to them. A substance is said to be crystalline when the arrangement of the units (atoms, molecules or ions) of matter inside it is regular and periodic.
Space lattice
An array of points which describe the three dimensional arrangement of particles (atoms, molecules or ions) in a crystal structure is called space lattice. Here environment about each point should be identical.
Basis
A crystal structure is formed by associating with every lattice point a unit assembly of units or molecules identical in composition. This unit assembly is called basis.
A crystal structure is formed by the addition of a basis to every lattice point.
I.e., lattice + Basis = crystal structure.
Thus the crystal structure is real and the crystal lattice is imaginary.




We can imagine two ways of identifying the unit cell in this structure. One is, with a1 and b1 as the basis vectors in which case, the unit cell will be a parallelogram. Here four lattice points are located at the vertices. This is a primitive cell. Other one is with the basis vectors a2 and b2 which would make a rectangle for the unit cell. Here in addition to the 4 points at the corners, one lattice point is at the centre. This is a nonprimitive cell.
Crystal systems
Bravais demonstrated mathematically that in 3-dimensions, there are only 14 different types of arrangements possible. These 14 Bravais lattices are classified into the seven crystal systems on the basis of relative lengths of basis vectors and interfacial angles.
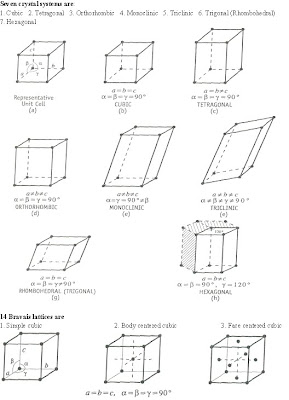


Crystal systems
Bravais demonstrated mathematically that in 3-dimensions, there are only 14 different types of arrangements possible. These 14 Bravais lattices are classified into the seven crystal systems on the basis of relative lengths of basis vectors and interfacial angles.



Many physical properties of crystalline solids are dependent on the direction of measurement or the planes across which the properties are studied. In order to specify directions in a lattice, we make use of lattice basis vectors a, b and c.
In general, any directional vector can be expressed as
R= n1a+n2b+n3c
where n1, n2 and n3 are integers. The direction of the vector R is determined by these integers. If these numbers have common factors, they are removed and the direction of R is denoted as [n1 n2 n3]. A similar set of three integers enclosed in a round bracket is used to designate planes in a crystal.
Lattice planes and Miller indices
The crystal lattice may be regarded as made up of a set of parallel, equidistant planes passing through the lattice points. These planes are known as lattice planes and may be represented by a set of three smallest possible integers. These numbers are called ‘Miller indices’ named after the crystallographer W.H.Miller.



In general, any directional vector can be expressed as
R= n1a+n2b+n3c
where n1, n2 and n3 are integers. The direction of the vector R is determined by these integers. If these numbers have common factors, they are removed and the direction of R is denoted as [n1 n2 n3]. A similar set of three integers enclosed in a round bracket is used to designate planes in a crystal.
Lattice planes and Miller indices
The crystal lattice may be regarded as made up of a set of parallel, equidistant planes passing through the lattice points. These planes are known as lattice planes and may be represented by a set of three smallest possible integers. These numbers are called ‘Miller indices’ named after the crystallographer W.H.Miller.



Number of atoms per unit cell (n)
1. Simple cubic lattice
There are eight corner atoms. Each corner atom is shared by eight unit cells. Hence the share of each unit cell is equal to one eighth of an atom. Therefore the total number of atom in one unit cell = 8 x 1/8 = 1.
2. Body centered cubic lattice
There are eight atoms at the eight corners of the unit cell and one atom at the body centre. As each corner atom is shared by eight unit cells, the contribution to each cell is 8 x 1/8 =1. Moreover, there is one body centre atom per unit cell. Therefore total number of atoms per unit cell= 1+1 = 2.
3. Face centered cubic lattice
There are eight atoms at the eight corners of the unit cell and six face centered atoms at the centre of six faces. As each corner atom is shared by eight unit cells, the contribution to each cell is 8 x 1/8 =1. Each face centered atom is shared by two unit cells. Hence the contribution of six face centered atoms to each unit cell is 6 x ½ = 3. Therefore the total number of atoms per unit cell = 1 + 3 = 4.
Co-ordination number
Co-ordination number is the number of equidistant neighbours surrounding an atom in the given crystal structure. When the coordination number is larger, the structure is more closely packed.
1. Simple cubic lattice
Here any corner atom has four nearest neighbours in the same plane and two nearest neighbours in a vertical plane. Hence co-ordination number in this case is six.
2. Body centered cubic lattice
For any corner atom of the unit cell, the nearest atoms are the atoms which are at the centers of unit cells. A corner atom is surrounded by eight unit cells having eight body centered atoms. Hence co-ordination number is eight.
3. Face centered cubic lattice
For any corner atom, there will be four face centered atoms of the surrounding unit cells in its own plane as nearest neighbours and four face centered atoms each in two perpendicular planes. Hence co-ordination number is 4 + 4 + 4 = 12.
Relation between atomic radius and the lattice constant
Atoms touch each other at least in one direction in a unit cell. All atoms could be assumed to be spherical in shape.




Crystal structure of NaCl
The crystal structure of NaCl is shown in figure:
1. Simple cubic lattice
There are eight corner atoms. Each corner atom is shared by eight unit cells. Hence the share of each unit cell is equal to one eighth of an atom. Therefore the total number of atom in one unit cell = 8 x 1/8 = 1.
2. Body centered cubic lattice
There are eight atoms at the eight corners of the unit cell and one atom at the body centre. As each corner atom is shared by eight unit cells, the contribution to each cell is 8 x 1/8 =1. Moreover, there is one body centre atom per unit cell. Therefore total number of atoms per unit cell= 1+1 = 2.
3. Face centered cubic lattice
There are eight atoms at the eight corners of the unit cell and six face centered atoms at the centre of six faces. As each corner atom is shared by eight unit cells, the contribution to each cell is 8 x 1/8 =1. Each face centered atom is shared by two unit cells. Hence the contribution of six face centered atoms to each unit cell is 6 x ½ = 3. Therefore the total number of atoms per unit cell = 1 + 3 = 4.
Co-ordination number
Co-ordination number is the number of equidistant neighbours surrounding an atom in the given crystal structure. When the coordination number is larger, the structure is more closely packed.
1. Simple cubic lattice
Here any corner atom has four nearest neighbours in the same plane and two nearest neighbours in a vertical plane. Hence co-ordination number in this case is six.
2. Body centered cubic lattice
For any corner atom of the unit cell, the nearest atoms are the atoms which are at the centers of unit cells. A corner atom is surrounded by eight unit cells having eight body centered atoms. Hence co-ordination number is eight.
3. Face centered cubic lattice
For any corner atom, there will be four face centered atoms of the surrounding unit cells in its own plane as nearest neighbours and four face centered atoms each in two perpendicular planes. Hence co-ordination number is 4 + 4 + 4 = 12.
Relation between atomic radius and the lattice constant
Atoms touch each other at least in one direction in a unit cell. All atoms could be assumed to be spherical in shape.




Crystal structure of NaCl
The crystal structure of NaCl is shown in figure:
NaCl is an example of face centered cubic lattice. NaCl is an ionic compound and Na+ and Cl- ions occupy alternate positions in the lattice. Thus there are four Na+ and Cl- ion pairs (molecules) per unit cell. If a corner Na+ ion is taken as origin, the position co-ordinates of Na+ and Cl- ions are as follows:
Na+ 0 0 0 ½ ½ 0 ½ 0 ½ 0 ½ ½
Cl- ½ ½ ½ 0 0 ½ 0 ½ 0 ½ 0 0
Lattice constant is related to the atomic radius R through the relation a = (8/Root3) R
The number of molecules per unit cell is 4 and the coordination number is 6.
Interatomic distance is 2.813 Å.
KCl, PbS, MnO and AgBr possess crystal structure identical to NaCl.
Crystal structure Diamond
The diamond lattice is composed of two interpenetrating face centered cubic sub lattices, one of which shifted relative to the other by one fourth of a body diagonal as shown:
The position co-ordinates of carbon atoms are
0 0 0 ½ ½ 0 ½ 0½ 0 ½½ ¼ ¼ ¼
Lattice constant is related to the atomic radius R through the relation a = (8/root3) R
The number of atoms per unit cell is 8 and the coordination number is 4.
Packing fraction is root3pi/16.
Ge and Si possess diamond structure.

Na+ 0 0 0 ½ ½ 0 ½ 0 ½ 0 ½ ½
Cl- ½ ½ ½ 0 0 ½ 0 ½ 0 ½ 0 0
Lattice constant is related to the atomic radius R through the relation a = (8/Root3) R
The number of molecules per unit cell is 4 and the coordination number is 6.
Interatomic distance is 2.813 Å.
KCl, PbS, MnO and AgBr possess crystal structure identical to NaCl.
Crystal structure Diamond
The diamond lattice is composed of two interpenetrating face centered cubic sub lattices, one of which shifted relative to the other by one fourth of a body diagonal as shown:
The position co-ordinates of carbon atoms are
0 0 0 ½ ½ 0 ½ 0½ 0 ½½ ¼ ¼ ¼
Lattice constant is related to the atomic radius R through the relation a = (8/root3) R
The number of atoms per unit cell is 8 and the coordination number is 4.
Packing fraction is root3pi/16.
Ge and Si possess diamond structure.







No comments:
Post a Comment